Recently I was doing some research regarding calculations for close-focus photography. Since I didn’t come across a place that collected all the relevant formulas (aside from a few forum posts), I thought I’d compile them a bit.
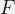 : Focal length
: Focal length
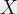 : Extension
: Extension
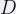 : Focused distance (measured from the lens nodal point)
: Focused distance (measured from the lens nodal point)
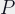 : Focused distance (measured from the film plane)
: Focused distance (measured from the film plane)
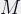 : Magnification
: Magnification
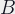 : Bellows factor
: Bellows factor
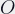 : Object size
: Object size
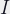 : Image size (size of
: Image size (size of 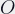 on film)
on film)
Focal length, extension and distance
First, the relationship between focal length, extension and distance. Extension is how far the nodal point of the lens is from the film plane. Note that this is at least the focal length of the lens1. An extension of 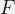 gives you infinity focus, more extension gets you closer.
gives you infinity focus, more extension gets you closer.
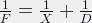
Magnification
Magnification is the relationship between the size of the subject, and the size it will be on film. With a magnification of 1, a 10mm subject will be 10mm on the film. Note that for macro lenses, magnification is often given in the form 1:(1/M), so a magnification of 0.5 would be 1:2, and life-size would be 1:1. magnifications bigger than 1 will have the bigger number in front, so a magnification of 2 would be 2:1.
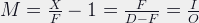
Note that you can invert this to find how small an item you can photograph with a given magnification. Using a 1:2 lens on 35mm film will allow you to photograph a scene of 72mm wide and 48mm high, for example.
Bellows factor
Bellows factor determines how much extra exposure is needed when photographing close to the camera2. Multiply the `normal’ exposure of the scene by the bellows factor to get the correct exposure.

Note that this only applies if you are using a camera without TTL metering. A TTL meter will automatically correct for this.
Some examples
Say I have a 135mm lens, that normally focusses down to 0.9 meters from the lens. The maximum magnification is then:
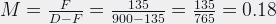
I can calculate the lens extension at closest focus:
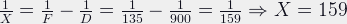
If I add a 25mm extension ring between the lens and the camera, I can calculate the new magnification at infinity:
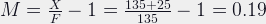
And the new magnification at closest focus:
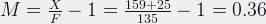
So with the extension ring, the lens becomes capable of roughly 1:3 macro.
If I were using a camera without TTL metering, I’d have to calculate the new exposure:
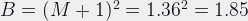
So I’d have to add about two-thirds of a stop to the exposure my meter sees in order to get a correctly exposed picture.
Without the macro ring, at closest focus the bellows factor would be:
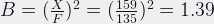
Which would be roughly one-third of a stop.
You can see that bellows factor doesn’t really become an issue until you get at 1:2 magnification or greater, from which point is increases very quickly.
It’s worth to note that the distance scales on most lenses indicate distance from the film plane, not from the focal point of the lens. This makes the calculations a lot more complex, as
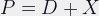
which converts the first formula above to:
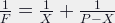
Imagine the lens mentioned above doen’t focus 0.9 meters from the lens, but from the film plane. It’s now not as easy to determine X. Rewriting the formula above, we get a quadratic formula:
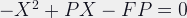
which our math teacher taught us means that:
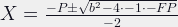
And thus:
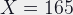
from there on, we can use the formulas above to determine magnification, bellows factor and everything else as normal.
Note that the quadratic formula also gives us
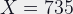
which is another extension that would give a subject to film-plane distance of 0.9 meters, though that would take us very solidly into macro territory, with a magnification of:
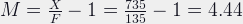
In other words: Well over four times life-size, and the exact reciprocal of the magnification at 165mm.
This is logical, since
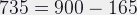
This is simply the entire optical system reversed, with the subject and film switching places.